WebGL2 二维旋转
此文上接一系列文章,先从基础概念开始 ,上一篇是 物体平移.
我承认我不知道怎么解释比较好,但是管它呢!先试试吧。
首先我想向你介绍一个叫做“单位圆”的东西。如果你还记得初中数学的话(别睡着了啊~喂!), 一个圆有一个半径,圆的半径是圆心到圆边缘的距离。单位圆是半径为 1.0 的圆。
这里有个单位圆。
当你拖拽蓝色圆点的时候 X 和 Y 会改变,它们是那一点在圆上的坐标, 在最上方时 Y 是 1 并且 X 是 0 ,在最右边的时候 X 是 1 并且 Y 是 0 。
如果你还记得三年级的数学知识,数字和 1 相乘结果不变。 例如 123 * 1 = 123 。非常基础,对吧?那么,单位圆,半径为 1.0 的圆也是 1 的一种形式,它是旋转的 1 。所以你可以把一些东西和单位圆相乘, 除了发生一些魔法和旋转之外,某种程度上和乘以 1 相似。
我们将从单位元上任取一点,并将该点的 X 和 Y 与之前例子.
这是新的着色器。
#version 300 es
in vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
+uniform vec2 u_rotation;
void main() {
+ // 旋转位置
+ vec2 rotatedPosition = vec2(
+ a_position.x * u_rotation.y + a_position.y * u_rotation.x,
+ a_position.y * u_rotation.y - a_position.x * u_rotation.x);
// 加上平移
* vec2 position = rotatedPosition + u_translation;
...
更新 JavaScript,传递两个值进去。
...
+ var rotationLocation = gl.getUniformLocation(program, "u_rotation");
...
+ var rotation = [0, 1];
...
// 绘制场景
function drawScene() {
webglUtils.resizeCanvasToDisplaySize(gl.canvas);
// 告诉WebGL如何从裁剪空间对应到像素
gl.viewport(0, 0, gl.canvas.width, gl.canvas.height);
// 清空画布
gl.clearColor(0, 0, 0, 0);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
// 使用我们的程序
gl.useProgram(program);
// 绑定属性/缓冲
gl.bindVertexArray(vao);
// 在着色器中通过画布分辨率转换像素坐标为裁剪空间坐标
gl.uniform2f(resolutionUniformLocation, gl.canvas.width, gl.canvas.height);
// 设置颜色
gl.uniform4fv(colorLocation, color);
// 设置平移
gl.uniform2fv(translationLocation, translation);
+ // 设置旋转
+ gl.uniform2fv(rotationLocation, rotation);
// 绘制矩形
var primitiveType = gl.TRIANGLES;
var offset = 0;
var count = 18;
gl.drawArrays(primitiveType, offset, count);
}
这是结果,拖动圆形手柄来旋转或拖动滑块来平移。
为什么会这样?来看看数学公式。
rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;
假如你想旋转一个矩形,在开始旋转之前矩形右上角坐标是 3.0, 9.0 , 让我们在单位圆上以十二点方向为起点顺时针旋转 30 度后取一个点。
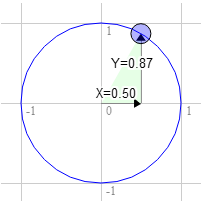
圆上该点的位置是 0.50 和 0.87
3.0 * 0.87 + 9.0 * 0.50 = 7.1 9.0 * 0.87 - 3.0 * 0.50 = 6.3
这个结果正好是我们需要的结果
顺时针 60 度也一样
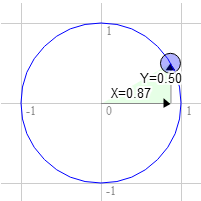
圆上该点的位置是 0.87 和 0.50 。
3.0 * 0.50 + 9.0 * 0.87 = 9.3 9.0 * 0.50 - 3.0 * 0.87 = 1.9
你会发现在我们顺时针旋转到右边的过程中,X 变大 Y 变小。如果我们继续旋转超过 90 度后,X 变小 Y 变大,这种形式形成了旋转。
单位圆上的点还有一个名字,叫做正弦和余弦。所以对于任意给定角, 我们只需要求出正弦和余弦,像这样
function printSineAndCosineForAnAngle(angleInDegrees) {
var angleInRadians = angleInDegrees * Math.PI / 180;
var s = Math.sin(angleInRadians);
var c = Math.cos(angleInRadians);
console.log("s = " + s + " c = " + c);
}
如果你吧代码复制到 JavaScript 控制台,然后输入 printSineAndCosignForAngle(30) ,
会打印出 s = 0.49 c = 0.87 (注意:我对结果四舍五入了)。
如果你把这些组合起来,就可以对几何体旋转任意角度,使用时只需要设置旋转的角度。
...
var angleInRadians = angleInDegrees * Math.PI / 180;
rotation[0] = Math.sin(angleInRadians);
rotation[1] = Math.cos(angleInRadians);
这里有一个设置角度的版本,拖动滑块来旋转或平移。
希望我解释的还过得去。 下一篇比较简单,缩放.