WebGL2 3D - 스팟 조명 효과(Spot Lighting)
이 글은 WebGL 3D 점 조명 효과에서 이어지는 글입니다. 이전 글을 아직 읽지 않았다면 먼저 읽어 보시길 권장합니다.
지난 글에서는 물체의 모든 점마다 빛이 그 점을 향하는 방향 벡터를 계산하는 점 조명 효과에 대해 다뤘습니다. 그 이후 과정은 방향성 조명 효과와 동일한데, 표면의 법선(표면이 바라보는 방향)과 조명 방향을 내적하는 것이었습니다. 두 방향이 동일한 경우 값이 1이되고, 완전히 비춰지게(fully lit) 됩니다. 만일 두 방향이 수직하다면 0이 되고, 반대라면 -1이 됩니다. 우리는 이 값을 표면의 색상에 직접 곱해서 조명 효과를 얻었습니다.
스팟 조명 효과(spot lighting)는 아주 약간 다를 뿐입니다. 사실 지금까지 해온 내용에 여러분이 약간의 창의력만 더하면 스스로 구현하는 방법을 찾으실 수 있을 겁니다.
점 조명은 어떤 위치에서 모든 방향으로 빛이 뻗어나가는 조명으로 생각할 수 있습니다. 스팟 조명을 구현하기 위해서는 위치를 중심으로 빛이 향하는 특정 방향을 정해야 합니다. 그리고 빛이 향하는 방향마다 그 방향과 우리가 정한 특정 방향와의 내적을 해 줍니다. 임의로 어떤 제한값을 정해서 제한값 이내이면 빛을 비추고, 제한값 밖이면 빛을 비추지 않도록 하는겁니다.
다이어그램에서 모든 방향으로 뻗어나가는 광선을 볼 수 있고, 각 광선에는 특정 방향과의 내적값이 표시되어 있습니다. 특정 방향은 스팟 조명의 방향입니다. 제한값을 정하면 (위쪽에 degree 단위로 나타내고 있습니다.) 그 제한값으로부터 내적 제한값을 계산하는데, 이는 제한값의 코사인 값입니다. 스팟 조명의 방향과 광선 방향을 내적했을 때 내적 제한값보다 크다면 빛을 비춥니다. 그렇지 않으면 비추지 않습니다.
다른 방식으로 설명해 보자면, 예를 들어 제한값이 20도라고 합시다. 이를 라디안으로 변환하고 코사인을 취해 -1과 1사이의 값으로 변환합니다. 이를 내적 공간이라고 합시다. 다시말해 아래 표와 같은 제한값이 있다고 합시다.
limits in
degrees | radians | dot space
--------+---------+----------
0 | 0.0 | 1.0
22 | .38 | .93
45 | .79 | .71
67 | 1.17 | .39
90 | 1.57 | 0.0
180 | 3.14 | -1.0
그러면 아래와 같은 체크를 하기만 하면 됩니다.
dotFromDirection = dot(surfaceToLight, -lightDirection)
if (dotFromDirection >= limitInDotSpace) {
// 조명 효과 계산
}
한번 해 봅시다.
먼저 지난 지난 글의 프래그먼트 셰이더를 수정합시다.
#version 300 es
precision highp float;
// 정점 셰이더에서 넘어온 값
in vec3 v_normal;
in vec3 v_surfaceToLight;
in vec3 v_surfaceToView;
uniform vec4 u_color;
uniform float u_shininess;
+uniform vec3 u_lightDirection;
+uniform float u_limit; // 내적 공간에서의 값
// 프래그먼트 셰이더에서는 출력값을 선언해야 합니다.
out vec4 outColor;
void main() {
// v_normal은 보간되는 varying 이기 때문에 단위 벡터가 아닙니다.
// 정규화를 해야 다시 단위 벡터가 됩니다.
vec3 normal = normalize(v_normal);
vec3 surfaceToLightDirection = normalize(v_surfaceToLight);
vec3 surfaceToViewDirection = normalize(v_surfaceToView);
vec3 halfVector = normalize(surfaceToLightDirection + surfaceToViewDirection);
- float light = dot(normal, surfaceToLightDirection);
+ float light = 0.0;
float specular = 0.0;
+ float dotFromDirection = dot(surfaceToLightDirection,
+ -u_lightDirection);
+ if (dotFromDirection >= u_limit) {
* light = dot(normal, surfaceToLightDirection);
* if (light > 0.0) {
* specular = pow(dot(normal, halfVector), u_shininess);
* }
+ }
outColor = u_color;
// 알파를 제외한 색상 부분만 light값을 곱해줍니다.
outColor.rgb *= light;
// specular 값을 더해줍니다.
outColor.rgb += specular;
}
당연히 방금 추가한 uniform들의 위치를 가지고 있어야 합니다.
var lightDirection = [?, ?, ?];
var limit = degToRad(20);
...
var lightDirectionLocation = gl.getUniformLocation(program, "u_lightDirection");
var limitLocation = gl.getUniformLocation(program, "u_limit");
그리고 값을 설정해 주어야 합니다.
gl.uniform3fv(lightDirectionLocation, lightDirection);
gl.uniform1f(limitLocation, Math.cos(limit));
결과는 아래와 같습니다.
몇 가지 주의사항입니다: 먼저 위 코드에서 u_lightDirection의 방향을 뒤집었다는 것입니다.
구현하는 방법은 두 가지가 있습니다. 우리가 필요한 건 비교하는 두 개의 방향이 동일하도록 맞춰주는 것입니다.
즉, surfaceToLightDirection과 스팟 조명의 반대 방향을 비교해야 한다는 것입니다.
여러가지 다른 방식으로 구현할 수 있는데, uniform 값을 설정할때 방향을 뒤집어서 전달해 줄 수도 있습니다.
저라면 이렇게 하겠지만 uniform을 u_lightDirection라고 이름짓는 것이
u_reverseLightDirection 또는 u_negativeLightDirection보다 덜 헷갈릴 것으로 생각됩니다.
다른 하나는 개인 선호도에 달린 것이긴 한데, 저는 가능하면 셰이더에 조건문을 사용하지 않으려 합니다. 아마도 그 이유는 실제로는 셰이더에 조건문이 없기 때문입니다. 셰이더에 조건문을 사용하게 되면 셰이더 컴파일러가 코드를 여기저기 0과 1을 곱하는 식으로 확장해서 실제로는 조건문이 없는 형태로 바꿉니다. 그 말은 조건문을 사용하면 조합하는 만큼 코드가 길어진다는 뜻입니다. 지금도 그런지는 확실하진 않지만 어쨋든 몇 가지 기술을 보여드리는 겸 해서 조건문을 없애 보겠습니다. 조건문을 사용할지 말지는 여러분이 스스로 결정하시면 됩니다.
GLSL에는 step이라는 함수가 있습니다.
2개의 값을 인자로 받는데 두 번째 값이 첫 번째 값보다 크거나 같으면 1.0을 반환합니다.
그렇지 않으면 0을 반환합니다. 아래 자바스크립트 코드처럼요.
function step(a, b) {
if (b >= a) {
return 1;
} else {
return 0;
}
}
조건문을 없애기 위해 step을 사용해 봅시다.
float dotFromDirection = dot(surfaceToLightDirection,
-u_lightDirection);
// spotLight 영역 안이면 inLight는 1이되고 아니면 0이 됩니다.
float inLight = step(u_limit, dotFromDirection);
float light = inLight * dot(normal, surfaceToLightDirection);
float specular = inLight * pow(dot(normal, halfVector), u_shininess);
보기에는 결과가 동일하지만 결과는 아래와 같습니다.
다른 하나는 스팟 라이트의 경계가 매우 거칠다는 것입니다. 스팟 라이트 영역 안에 있거나 밖에 있거나 둘 중 하나고 밖에 있다면 완전히 어둡습니다.
이것을 수정하기 위해서 하나의 경계값 대신 안쪽 경계값과 바깥쪽 경계값, 두 개의 경계값을 사용할 수 있습니다. 안쪽 경계값 안에 있으면 1.0을 사용합니다. 그리고 바깥쪽 경계값 밖에 있으면 0.0을 사용합니다. 안쪽 경계값과 바깥쪽 경계값 사이라면 1.0과 0.0 사이의 값을 lerp(linear interpolation)합니다.
아래는 구현 방법 중 하나입니다.
-uniform float u_limit; // 내적 공간에서의 값
+uniform float u_innerLimit; // 내적 공간에서의 값
+uniform float u_outerLimit; // 내적 공간에서의 값
...
float dotFromDirection = dot(surfaceToLightDirection,
-u_lightDirection);
- float inLight = step(u_limit, dotFromDirection);
+ float limitRange = u_innerLimit - u_outerLimit;
+ float inLight = clamp((dotFromDirection - u_outerLimit) / limitRange, 0.0, 1.0);
float light = inLight * dot(normal, surfaceToLightDirection);
float specular = inLight * pow(dot(normal, halfVector), u_shininess);
잘 동작하네요.
이제 좀 더 스팟 라이트처럼 보이는 결과를 얻었습니다!
하나 주의해야 할 것은 u_innerLimit와 u_outerLimit값이 같으면 limitRange값이 0.0이 된다는 것입니다.
이후 계산에서 limitRange로 나누는데, 0으로 나누는 것은 나쁜/정의되지 않은 결과가 도출됩니다.
셰이더 코드 안에서 우리가 무언가 할 수 있는것은 없고, 자바스크립트 코드 안에서 u_innerLimit와 u_outerLimit가 같은 값이 되지 않도록 해야 합니다. (주의: 예제 코드에서 이 작업을 하고 있지는 앖습니다.)
GLSL에도 이러한 작업을 약간 간단한게 할 수 있는 함수가 있습니다.
smoothstep이라는 함수인데 step처럼 0과 1 사이의 값을 반환하지만 하한값과 상한값을 모두 인자로 받아서 그 범위 안에서 lerp한 값을 반환합니다.
smoothstep(lowerBound, upperBound, value)
사용해 봅시다.
float dotFromDirection = dot(surfaceToLightDirection,
-u_lightDirection);
- float limitRange = u_innerLimit - u_outerLimit;
- float inLight = clamp((dotFromDirection - u_outerLimit) / limitRange, 0.0, 1.0);
float inLight = smoothstep(u_outerLimit, u_innerLimit, dotFromDirection);
float light = inLight * dot(normal, surfaceToLightDirection);
float specular = inLight * pow(dot(normal, halfVector), u_shininess);
마찬가지로 잘 동작합니다.
차이점이라면 smoothstep은 선형 보간 대신 hermite 보간을 한다는 것입니다.
그 말은 lowerBound와 upperBound 사이 값을 아래 오른쪽 그림처럼 보간한다는 것입니다.
반면 선형 보간은 아래 왼쪽 그림처럼 보간합니다.
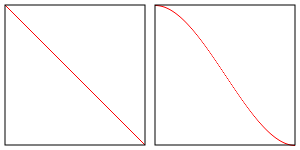
그 차이에 신경쓸 것인지 아닌지는 여러분에게 달려 있습니다.
하나 더 주의해야 할 것은 smoothstep함수는 lowerBound가 upperBound보다 크거나 같으면 정의되지 않은 결과가 도출됩니다.
두 값이 동일하면 위에서 언급한 것과 같은 동일한 문제가 발생합니다.
추가로 lowerBound가 upperBound보다 클 때 새로운 이슈가 발생하지만 스팟 조명의 목적상 이러한 경우는 없어야 합니다.