WebGL2 2D 회전
이 글은 WebGL 게시글 시리즈에서 이어지는 글입니다. 첫 번째는 기초로 시작이었으며 바로 전은 기하학에 대한 이동이였습니다.
I’m going to admit right up front I have no idea if how I explain this will make sense but what the heck, might as well try.
먼저 "단위 원(unit circle)"라고 불리는 것을 소개 하고자 합니다. 만약 중학교 수학을 기억한다면(잠자면 안됩니다!) 원은 반지름(radius)을 가지고 있습니다. 원의 반지름(radius)은 원의 중심으로 부터 원의 가장자리 까지의 거리입니다. 단위 원은 반지름(radius)이 1인 원 입니다.
여기에 단위 원이 있습니다.
파란색 핸들을 원 주위로 드래그하면 X 와 Y의 위치가 변경됩니다. 이는 보여 원위의 그 지점의 위치를 나타냅니다. 상단에서 Y는 1이고 X는 0입니다. 오른쪽에서 X는 1이고 Y는 0입니다.
초등학교 3학년 수학에서 무언가에 1을 곱하면 같은 값을 유지한다는 것을 기억할 것입니다. 그러므로 123 * 1 = 123. 아주 기본이죠? 단위원에서 반지름이 1.0인 것도 1입니다. 회전할때도 1입니다. 그러므로 이 단위원으로 무언가를 곱할수 있고 마술이 일어나서 회전하는것 뺴고는 1을 곱하는것과 같습니다.
단위 원에 임의의 점 X와 Y를 정할것이고 전에 했던 예제에 지오메트리(geometry)에 곱할것입니다.
여기에 업데이트된 쉐이더가 있습니다.
#version 300 es
in vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
+uniform vec2 u_rotation;
void main() {
+ // 위치 회전
+ vec2 rotatedPosition = vec2(
+ a_position.x * u_rotation.y + a_position.y * u_rotation.x,
+ a_position.y * u_rotation.y - a_position.x * u_rotation.x);
// 이동 추가
* vec2 position = rotatedPosition + u_translation;
...
그리고 자바스크립트를 업데이트하여 이 두 값을 전달할 수 있게 합니다.
...
+ var rotationLocation = gl.getUniformLocation(program, "u_rotation");
...
+ var rotation = [0, 1];
...
// scene 그리기.
function drawScene() {
webglUtils.resizeCanvasToDisplaySize(gl.canvas);
// WebGL에 클립 공간에서 픽셀로 변환하는 방법을 전달합니다.
gl.viewport(0, 0, gl.canvas.width, gl.canvas.height);
// 캔버스 지우기
gl.clearColor(0, 0, 0, 0);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
// 사용할 프로그램(쉐이더 쌍)을 전달합니다
gl.useProgram(program);
// 원하는 속성(attribute)/버퍼(buffer)를 연결 합니다.
gl.bindVertexArray(vao);
// 캔버스로 해상도를 쉐이더의 픽셀에서 클립공간으로 변환 할수 있게 전달합니다.
gl.uniform2f(resolutionUniformLocation, gl.canvas.width, gl.canvas.height);
// 색상 설정
gl.uniform4fv(colorLocation, color);
// 이동 설정
gl.uniform2fv(translationLocation, translation);
+ // 회전 설정
+ gl.uniform2fv(rotationLocation, rotation);
// 사각형 그리기
var primitiveType = gl.TRIANGLES;
var offset = 0;
var count = 18;
gl.drawArrays(primitiveType, offset, count);
}
여기에 결과가 있습니다. 회전하기 위해 원의 핸들을 드래그하거나 이동하기 위해 슬라이더를 드래그하십시오.
왜 작동할까요? 음, 수학을 봐 봅시다.
rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;
직사각형이 있고 회전하려고 한다고 가정해 보겠습니다. 회전하기 전에 오른쪽 위 구석이 3.0, 9.0에 있습니다. 12 방향에서 시계 방향으로 30도 단위 점을 찍어 봅시다.
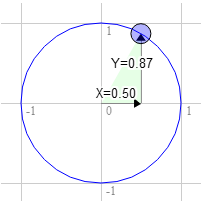
원에서 위치는 0.5와 0.87입니다.
3.0 * 0.87 + 9.0 * 0.50 = 7.1 9.0 * 0.87 - 3.0 * 0.50 = 6.3
이것이 바로 우리가 필요한 것 입니다.
시계 방향으로 60도 회전도 똑같습니다.
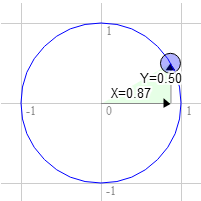
원에서 위치는 0.87과 0.5입니다.
3.0 * 0.50 + 9.0 * 0.87 = 9.3 9.0 * 0.50 - 3.0 * 0.87 = 1.9
점을 시계 방향으로 오른쪽으로 돌릴 때 X 값이 커지고 Y 값이 작아지는 것을 볼 수 있습니다. 90도를 지나 가면 X는 다시 작아지고 Y는 점점 커질 것입니다. 이 패턴이 회전으로 제공됩니다.
단위원의 점에 대한 또 다른 이름이 있습니다. 사인과 코사인이라고 불리는 것입니다. 주어진 각도에 대하여 다음과 같이 사인과 코사인을 찾을 수 있습니다.
function printSineAndCosineForAnAngle(angleInDegrees) {
var angleInRadians = angleInDegrees * Math.PI / 180;
var s = Math.sin(angleInRadians);
var c = Math.cos(angleInRadians);
console.log("s = " + s + " c = " + c);
}
자바스크립트 콘솔에 코드를 복사하고 붙여넣고 printSineAndCosineForAnAngle(30)을 실행하면, (반올림해서 적으면) s = 0.49 c = 0.87을 볼 수 있습니다.
이 모든 것들을 함께 사용하면 원하는 각도로 지오메트리(geometry)를 회전시킬 수 있습니다. 회전하려는 각도의 사인 및 코사인으로 회전을 설정하면됩니다.
...
var angleInRadians = angleInDegrees * Math.PI / 180;
rotation[0] = Math.sin(angleInRadians);
rotation[1] = Math.cos(angleInRadians);
아래는 각도를 조정할 수 있는 버전입니다. 원을 움직여서 회전시키거나, 슬라이더를 드래그하여 이동시켜보세요.
이해가 됐기를 바랍니다. 다음은, 더 간단한 "크기 변환"입니다..