This article is a continuation of WebGL 3D Point Lighting. If you haven't read that I suggest you start there.

In the last article we covered point lighting where for every point on the surface of our object we compute the direction from the light to that point on the surface. We then do the same thing we did for directional lighting which is we took the dot product of the surface normal (the direction the surface is facing) and the light direction. This gave us a value of 1 if the two directions matched and should therefore be fully lit. 0 if the two directions were perpendicular and -1 if they were opposite. We used that value directly to multiply the color of the surface which gave us lighting.

Spot lighting is only a very small change. In fact if you think creatively about the stuff we've done so far you might be able to derive your own solution.

You can imagine a point light as a point with light going in all directions from that point. To make a spot light all we need to do is choose a direction from that point, this is the direction of our spotlight. Then, for every direction the light is going we could take the dot product of that direction with our chosen spotlight direction. We'd pick some arbitrary limit and decide if we're within that limit we light. If we're not within that limit we don't light.

In the diagram above we can see a light with rays going in all directions and printed on them is their dot product relative to the direction. We then have a specific direction that is the direction of the spotlight. We choose a limit (above it's in degrees). From the limit we compute a dot limit, we just take the cosine of the limit. If the dot product of our chosen direction of the spotlight to the direction of each ray of light is above the dot limit then we do the lighting. Otherwise no lighting.

To say this another way, let's say the limit is 20 degrees. We can convert that to radians and from that to a value for -1 to 1 by taking the cosine. Let's call that dot space. In other words here's a small table for limit values

          limits in
 degrees | radians | dot space
 --------+---------+----------
    0    |   0.0   |    1.0
    22   |    .38  |     .93
    45   |    .79  |     .71
    67   |   1.17  |     .39
    90   |   1.57  |    0.0
   180   |   3.14  |   -1.0

Then we can the just check

dotFromDirection = dot(surfaceToLight, -lightDirection)
if (dotFromDirection >= limitInDotSpace) {
   // do the lighting
}

Let's do that

First let's modify our fragment shader from the last article.

#version 300 es
precision highp float;

// Passed in from the vertex shader.
in vec3 v_normal;
in vec3 v_surfaceToLight;
in vec3 v_surfaceToView;

uniform vec4 u_color;
uniform float u_shininess;
+uniform vec3 u_lightDirection;
+uniform float u_limit;          // in dot space

// we need to declare an output for the fragment shader
out vec4 outColor;

void main() {
  // because v_normal is a varying it's interpolated
  // so it will not be a unit vector. Normalizing it
  // will make it a unit vector again
  vec3 normal = normalize(v_normal);

  vec3 surfaceToLightDirection = normalize(v_surfaceToLight);
  vec3 surfaceToViewDirection = normalize(v_surfaceToView);
  vec3 halfVector = normalize(surfaceToLightDirection + surfaceToViewDirection);

-  float light = dot(normal, surfaceToLightDirection);
+  float light = 0.0;
  float specular = 0.0;

+  float dotFromDirection = dot(surfaceToLightDirection,
+                               -u_lightDirection);
+  if (dotFromDirection >= u_limit) {
*    light = dot(normal, surfaceToLightDirection);
*    if (light > 0.0) {
*      specular = pow(dot(normal, halfVector), u_shininess);
*    }
+  }

  outColor = u_color;

  // Lets multiply just the color portion (not the alpha)
  // by the light
  outColor.rgb *= light;

  // Just add in the specular
  outColor.rgb += specular;
}

Of course we need to look up the locations of the uniforms we just added.

  var lightDirection = [?, ?, ?];
  var limit = degToRad(20);

  ...

  var lightDirectionLocation = gl.getUniformLocation(program, "u_lightDirection");
  var limitLocation = gl.getUniformLocation(program, "u_limit");

and we need to set them

    gl.uniform3fv(lightDirectionLocation, lightDirection);
    gl.uniform1f(limitLocation, Math.cos(limit));

And here it is

A few things to note: One is we're negating u_lightDirection above. That's a six of one, half dozen of another type of thing. We want the 2 directions we're comparing to point in the same direction when they match. That means we need to compare the surfaceToLightDirection to the opposite of the spotlight direction. We could do this in many different ways. We could pass the negative direction when setting the uniform. This would be my 1st choice but I thought it would be less confusing to call the uniform u_lightDirection instead of u_reverseLightDirection or u_negativeLightDirection

Another thing, and maybe this is just a personal preference, I don't like to use conditionals in shaders if possible. I think the reason is it used to be that shaders didn't actually have conditionals. If you added a conditional the shader compiler would expand the code with lots of multiply by 0 and 1 here and there to make it so there were not any actual conditionals in the code. That meant adding conditionals could make your code explode into combinatorial expansions. I'm not sure that's true anymore but let's get rid of the conditionals anyway just to show some techniques. You can decide yourself whether or not to use them.

There is a GLSL function called step. It takes 2 values and if the second value is greater than or equal the first it returns 1.0. Otherwise it returns 0. You could write it like this in JavaScript

function step(a, b) {
   if (b >= a) {
       return 1;
   } else {
       return 0;
   }
}

Let's use step to get rid of the conditions

  float dotFromDirection = dot(surfaceToLightDirection,
                               -u_lightDirection);
  // inLight will be 1 if we're inside the spotlight and 0 if not
  float inLight = step(u_limit, dotFromDirection);
  float light = inLight * dot(normal, surfaceToLightDirection);
  float specular = inLight * pow(dot(normal, halfVector), u_shininess);

Nothing changes visually but here is that

One other thing is right now the spotlight is super harsh. We're either inside the spotlight or not and things just turn black.

To fix this we could use 2 limits instead of one, an inner limit and an outer limit. If we're inside the inner limit then use 1.0. If we're outside the outer limit then use 0.0. If we're between the inner limit and the outer limit then lerp between 1.0 and 0.0.

Here's one way we could do this

-uniform float u_limit;          // in dot space
+uniform float u_innerLimit;     // in dot space
+uniform float u_outerLimit;     // in dot space

...

  float dotFromDirection = dot(surfaceToLightDirection,
                               -u_lightDirection);
-  float inLight = step(u_limit, dotFromDirection);
+  float limitRange = u_innerLimit - u_outerLimit;
+  float inLight = clamp((dotFromDirection - u_outerLimit) / limitRange, 0.0, 1.0);
  float light = inLight * dot(normal, surfaceToLightDirection);
  float specular = inLight * pow(dot(normal, halfVector), u_shininess);

And that works

Now we're getting something that looks more like a spotlight!

One thing to be aware of is if u_innerLimit is equal to u_outerLimit then limitRange will be 0.0. We divide by limitRange and dividing by zero is bad/undefined. There's nothing to do in the shader here we just need to make sure in our JavaScript that u_innerLimit is never equal to u_outerLimit. (note: the example code does not do this).

GLSL also has a function we could use to slightly simplify this. It's called smoothstep and like step it returns a value from 0 to 1 but it takes both an lower and upper bound and lerps between 0 and 1 between those bounds.

 smoothstep(lowerBound, upperBound, value)

Let's do that

  float dotFromDirection = dot(surfaceToLightDirection,
                               -u_lightDirection);
-  float limitRange = u_innerLimit - u_outerLimit;
-  float inLight = clamp((dotFromDirection - u_outerLimit) / limitRange, 0.0, 1.0);
  float inLight = smoothstep(u_outerLimit, u_innerLimit, dotFromDirection);
  float light = inLight * dot(normal, surfaceToLightDirection);
  float specular = inLight * pow(dot(normal, halfVector), u_shininess);

That works too

The difference is smoothstep uses a hermite interpolation instead of a linear interpolation. That means between lowerBound and upperBound it interpolates like the image below on the right whereas a linear interpolation is like the image on the left.

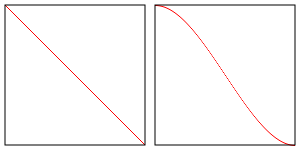
It's up to you if you think the difference matters.

One other thing to be aware is the smoothstep function has undefined results if the lowerBound is greater than or equal to upperBound. Having them be equal is the same issue we had above. The added issue of not being defined if lowerBound is greater than upperBound is new but for the purpose of a spotlight that should never be true.

genType asin (genType x)

genType acos (genType x)

genType atan (genType y, genType x)

genType acosh (genType x)

genType atanh (genType x)

genType pow (genType x, genType y)

genType log (genType x)

genType log2 (genType x)

genType sqrt (genType x)

genType inversesqrt (genType x)

genType clamp (genType x, genType minVal, genType maxVal)
genType clamp (genType x, float minVal, float maxVal)

genType smoothstep (genType edge0, genType edge1, genType x)
genType smoothstep (float edge0, float edge1, genType x)

 genType t;
 t = clamp ((x – edge0) / (edge1 – edge0), 0, 1);
 return t * t * (3 – 2 * t);

mat2 inverse(mat2 m)
mat3 inverse(mat3 m)
mat4 inverse(mat4 m)