WebGL2 3D - Прожекторное освещение
Эта статья является продолжением WebGL 3D Точечное освещение. Если вы не читали это, я предлагаю начать там.
В последней статье мы рассмотрели точечное освещение, где для каждой точки на поверхности нашего объекта мы вычисляем направление от света к этой точке на поверхности. Затем мы делаем то же самое, что делали для направленного освещения, что мы взяли скалярное произведение нормали поверхности (направление, в котором обращена поверхность) и направления света. Это дало нам значение 1, если два направления совпадали и поэтому должны быть полностью освещены. 0, если два направления были перпендикулярны, и -1, если они были противоположны. Мы использовали это значение напрямую для умножения цвета поверхности, что дало нам освещение.
Прожекторное освещение - это только очень небольшое изменение. На самом деле, если вы думаете творчески о том, что мы сделали до сих пор, вы могли бы вывести собственное решение.
Вы можете представить точечный свет как точку со светом, идущим во всех направлениях от этой точки. Чтобы сделать прожектор, все, что нам нужно сделать, это выбрать направление от этой точки, это направление нашего прожектора. Затем, для каждого направления, в котором идет свет, мы могли бы взять скалярное произведение этого направления с нашим выбранным направлением прожектора. Мы бы выбрали какой-то произвольный предел и решили, если мы в пределах этого предела, мы освещаем. Если мы не в пределах предела, мы не освещаем.
В диаграмме выше мы можем видеть свет с лучами, идущими во всех направлениях, и напечатанными на них их скалярными произведениями относительно направления. Затем у нас есть конкретное направление, которое является направлением прожектора. Мы выбираем предел (выше он в градусах). Из предела мы вычисляем dot limit, мы просто берем косинус предела. Если скалярное произведение нашего выбранного направления прожектора к направлению каждого луча света выше dot limit, то мы делаем освещение. Иначе нет освещения.
Чтобы сказать это по-другому, скажем, предел составляет 20 градусов. Мы можем преобразовать это в радианы и от этого к значению от -1 до 1, взяв косинус. Давайте назовем это dot space. Другими словами, вот небольшая таблица для значений предела
пределы в
градусах | радианах | dot space
--------+---------+----------
0 | 0.0 | 1.0
22 | .38 | .93
45 | .79 | .71
67 | 1.17 | .39
90 | 1.57 | 0.0
180 | 3.14 | -1.0
Затем мы можем просто проверить
dotFromDirection = dot(surfaceToLight, -lightDirection)
if (dotFromDirection >= limitInDotSpace) {
// делаем освещение
}
Давайте сделаем это
Сначала давайте изменим наш фрагментный шейдер из последней статьи.
#version 300 es
precision highp float;
// Переданный из вершинного шейдера.
in vec3 v_normal;
in vec3 v_surfaceToLight;
in vec3 v_surfaceToView;
uniform vec4 u_color;
uniform float u_shininess;
+uniform vec3 u_lightDirection;
+uniform float u_limit; // в dot space
// нам нужно объявить выход для фрагментного шейдера
out vec4 outColor;
void main() {
// потому что v_normal - это varying, он интерполируется
// поэтому он не будет единичным вектором. Нормализация его
// сделает его снова единичным вектором
vec3 normal = normalize(v_normal);
vec3 surfaceToLightDirection = normalize(v_surfaceToLight);
vec3 surfaceToViewDirection = normalize(v_surfaceToView);
vec3 halfVector = normalize(surfaceToLightDirection + surfaceToViewDirection);
- float light = dot(normal, surfaceToLightDirection);
+ float light = 0.0;
float specular = 0.0;
+ float dotFromDirection = dot(surfaceToLightDirection,
+ -u_lightDirection);
+ if (dotFromDirection >= u_limit) {
* light = dot(normal, surfaceToLightDirection);
* if (light > 0.0) {
* specular = pow(dot(normal, halfVector), u_shininess);
* }
+ }
outColor = u_color;
// Давайте умножим только цветовую часть (не альфа)
// на свет
outColor.rgb *= light;
// Просто добавляем блик
outColor.rgb += specular;
}
Конечно, нам нужно найти местоположения uniform переменных, которые мы только что добавили.
var lightDirection = [?, ?, ?];
var limit = degToRad(20);
...
var lightDirectionLocation = gl.getUniformLocation(program, "u_lightDirection");
var limitLocation = gl.getUniformLocation(program, "u_limit");
и нам нужно их установить
gl.uniform3fv(lightDirectionLocation, lightDirection);
gl.uniform1f(limitLocation, Math.cos(limit));
И вот это
Несколько вещей для заметки: Одна в том, что мы отрицаем u_lightDirection выше.
Это шесть одного, полдюжины другого
тип вещи. Мы хотим, чтобы 2 направления, которые мы сравниваем, указывали в
том же направлении, когда они совпадают. Это означает, что нам нужно сравнить
surfaceToLightDirection с противоположным направлением прожектора.
Мы могли бы сделать это многими разными способами. Мы могли бы передать отрицательное
направление при установке uniform. Это был бы мой 1-й выбор,
но я думал, что будет менее запутанно назвать uniform u_lightDirection вместо u_reverseLightDirection или u_negativeLightDirection
Другая вещь, и, возможно, это просто личное предпочтение, я не люблю использовать условные операторы в шейдерах, если возможно. Я думаю, причина в том, что раньше шейдеры на самом деле не имели условных операторов. Если вы добавляли условный оператор, компилятор шейдера расширял код множеством умножений на 0 и 1 здесь и там, чтобы сделать так, чтобы не было никаких фактических условных операторов в коде. Это означало, что добавление условных операторов могло заставить ваш код взорваться в комбинаторные расширения. Я не уверен, что это все еще правда, но давайте избавимся от условных операторов в любом случае, просто чтобы показать некоторые техники. Вы можете сами решить, использовать их или нет.
Есть функция GLSL, называемая step. Она принимает 2 значения, и если
второе значение больше или равно первому, она возвращает 1.0. Иначе она возвращает 0. Вы могли бы написать это так в JavaScript
function step(a, b) {
if (b >= a) {
return 1;
} else {
return 0;
}
}
Давайте используем step, чтобы избавиться от условий
float dotFromDirection = dot(surfaceToLightDirection,
-u_lightDirection);
// inLight будет 1, если мы внутри прожектора, и 0, если нет
float inLight = step(u_limit, dotFromDirection);
float light = inLight * dot(normal, surfaceToLightDirection);
float specular = inLight * pow(dot(normal, halfVector), u_shininess);
Ничего не меняется визуально, но вот это
Еще одна вещь в том, что сейчас прожектор очень резкий. Мы либо внутри прожектора, либо нет, и вещи просто становятся черными.
Чтобы исправить это, мы могли бы использовать 2 предела вместо одного, внутренний предел и внешний предел. Если мы внутри внутреннего предела, то используем 1.0. Если мы снаружи внешнего предела, то используем 0.0. Если мы между внутренним пределом и внешним пределом, то интерполируем между 1.0 и 0.0.
Вот один способ, как мы могли бы сделать это
-uniform float u_limit; // в dot space
+uniform float u_innerLimit; // в dot space
+uniform float u_outerLimit; // в dot space
...
float dotFromDirection = dot(surfaceToLightDirection,
-u_lightDirection);
- float inLight = step(u_limit, dotFromDirection);
+ float limitRange = u_innerLimit - u_outerLimit;
+ float inLight = clamp((dotFromDirection - u_outerLimit) / limitRange, 0.0, 1.0);
float light = inLight * dot(normal, surfaceToLightDirection);
float specular = inLight * pow(dot(normal, halfVector), u_shininess);
И это работает
Теперь мы получаем что-то, что выглядит больше как прожектор!
Одна вещь, о которой нужно знать, это если u_innerLimit равен u_outerLimit,
то limitRange будет 0.0. Мы делим на limitRange, и деление на
ноль плохо/не определено. Здесь нечего делать в шейдере, нам просто
нужно убедиться в нашем JavaScript, что u_innerLimit никогда не равен
u_outerLimit. (примечание: пример кода этого не делает).
GLSL также имеет функцию, которую мы могли бы использовать для небольшого упрощения этого. Она
называется smoothstep, и как step она возвращает значение от 0 до 1, но
она принимает как нижнюю, так и верхнюю границу и интерполирует между 0 и 1 между
этими границами.
smoothstep(lowerBound, upperBound, value)
Давайте сделаем это
float dotFromDirection = dot(surfaceToLightDirection,
-u_lightDirection);
- float limitRange = u_innerLimit - u_outerLimit;
- float inLight = clamp((dotFromDirection - u_outerLimit) / limitRange, 0.0, 1.0);
float inLight = smoothstep(u_outerLimit, u_innerLimit, dotFromDirection);
float light = inLight * dot(normal, surfaceToLightDirection);
float specular = inLight * pow(dot(normal, halfVector), u_shininess);
Это тоже работает
Разница в том, что smoothstep использует интерполяцию Эрмита вместо
линейной интерполяции. Это означает, что между lowerBound и upperBound
она интерполирует, как изображение ниже справа, тогда как линейная интерполяция, как изображение слева.
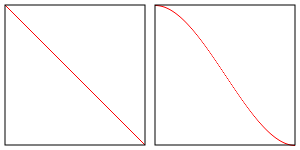
Вам решать, имеет ли значение разница.
Еще одна вещь, о которой нужно знать, это то, что функция smoothstep имеет неопределенные
результаты, если lowerBound больше или равен upperBound. Иметь
их равными - это та же проблема, что у нас была выше. Добавленная проблема не быть
определенным, если lowerBound больше upperBound, новая, но для
цели прожектора это никогда не должно быть правдой.