Это, вероятно, довольно специфическая тема, но я нашел её интересной, поэтому пишу об этом. Это не то, что я рекомендую вам делать на практике. Скорее, я думаю, что работа над этой темой поможет проиллюстрировать некоторые аспекты создания 3D моделей для WebGL.

Кто-то спросил, как создать форму кегли для боулинга в WebGL. Умный ответ: "Используйте 3D пакет моделирования, такой как Blender, Maya, 3D Studio Max, Cinema 4D, и т.д. Используйте его для моделирования кегли, экспортируйте, прочитайте данные. (Формат OBJ относительно прост).

Но это заставило меня задуматься, а что если они хотели создать пакет моделирования?

Есть несколько идей. Одна из них - создать цилиндр и попытаться сжать его в нужных местах, используя синусоидальные волны, примененные в определенных местах. Проблема с этой идеей в том, что вы не получите гладкую вершину. Стандартный цилиндр генерируется как серия равноудаленных колец, но вам понадобится больше колец там, где вещи более изогнуты.

В пакете моделирования вы бы создали кеглю, сделав 2D силуэт или, скорее, изогнутую линию, которая соответствует краю 2D силуэта. Затем вы бы выточили это в 3D форму. Под токарной обработкой я имею в виду, что вы бы вращали это вокруг некоторой оси и генерировали бы точки в процессе. Это позволяет легко создавать любые круглые объекты, такие как чаша, стакан, бейсбольная бита, бутылки, лампочки и т.д.

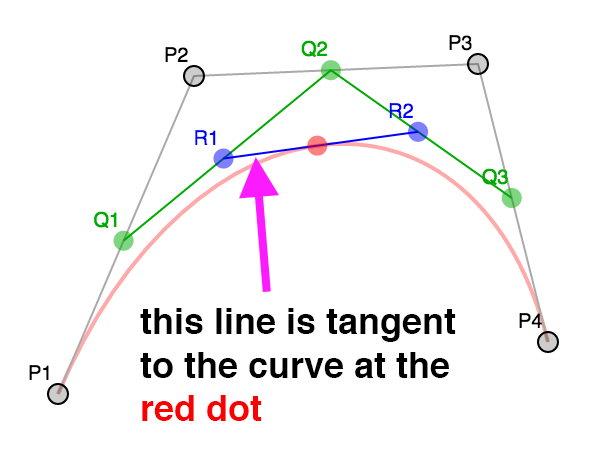
Итак, как мы это делаем? Ну, сначала нам нужен способ создать кривую. Затем нам нужно будет вычислить точки на этой кривой. Мы бы затем вращали эти точки вокруг некоторой оси, используя матричную математику, и строили треугольники из этих точек.

Самый распространенный вид кривой в компьютерной графике, кажется, кривая Безье. Если вы когда-либо редактировали кривую в Adobe Illustrator или Inkscape или Affinity Designer или подобных программах, это кривая Безье.

Кривая Безье, или скорее кубическая кривая Безье, формируется 4 точками. 2 точки - это конечные точки. 2 точки - это “контрольные точки”.

Вот 4 точки

Мы выбираем число между 0 и 1 (называемое t), где 0 = начало и 1 = конец. Затем мы вычисляем соответствующую точку t между каждой парой точек. P1 P2, P2 P3, P3 P4.

Другими словами, если t = .25, то мы вычисляем точку на 25% пути от P1 к P2, еще одну на 25% пути от P2 к P3 и еще одну на 25% пути от P3 к P4.

Вы можете перетащить ползунок, чтобы настроить t, и вы также можете перемещать точки P1, P2, P3 и P4.

Мы делаем то же самое для результирующих точек. Вычисляем точки t между Q1 Q2 и Q2 Q3.

Наконец, мы делаем то же самое для этих 2 точек и вычисляем точку t между R1 R2.

Позиции этой красной точки образуют кривую.

Итак, это кубическая кривая Безье.

Обратите внимание, что хотя интерполяция между точками выше и процесс создания 3 точек из 4, затем 2 из 3, и наконец 1 точки из 2 работает, это не обычный способ. Вместо этого кто-то подставил всю математику и упростил её до формулы, подобной этой

invT = (1 - t)
P = P1 * invT^3 +
    P2 * 3 * t * invT^2 +
    P3 * 3 * invT * t^2 +
    P4 * t^3

Где P1, P2, P3, P4 - это точки, как в примерах выше, а P

• это красная точка.

В 2D программе векторной графики, такой как Adobe Illustrator, когда вы создаете более длинную кривую, она фактически состоит из множества маленьких 4-точечных кривых, подобных этой. По умолчанию большинство приложений блокируют контрольные точки вокруг общей начальной/конечной точки и обеспечивают, чтобы они всегда были противоположны относительно общей точки.

Смотрите этот пример, переместите P3 или P5, и код переместит другой.

Обратите внимание, что кривая, созданная P1,P2,P3,P4, является отдельной кривой от той, что создана P4,P5,P6,P7. Просто когда P3 и P5 находятся на точных противоположных сторонах P4, вместе они выглядят как одна непрерывная кривая. Большинство приложений обычно дают вам возможность прекратить блокировку их вместе, чтобы вы могли получить острый угол. Снимите флажок блокировки, затем перетащите P3 или P5, и станет еще более ясно, что они являются отдельными кривыми.

Далее нам нужен способ генерировать точки на кривой. Используя формулу выше, мы можем сгенерировать точку для заданного значения t, как это.

function getPointOnBezierCurve(points, offset, t) {
  const invT = (1 - t);
  return v2.add(v2.mult(points[offset + 0], invT * invT * invT),
                v2.mult(points[offset + 1], 3 * t * invT * invT),
                v2.mult(points[offset + 2], 3 * invT * t * t),
                v2.mult(points[offset + 3], t * t  *t));
}

И мы можем сгенерировать набор точек для кривой, как это

function getPointsOnBezierCurve(points, offset, numPoints) {
  const cpoints = [];
  for (let i = 0; i < numPoints; ++i) {
    const t = i / (numPoints - 1);
    cpoints.push(getPointOnBezierCurve(points, offset, t));
  }
  return cpoints;
}

Примечание: v2.mult и v2.add - это маленькие JavaScript функции, которые я включил для помощи в математических операциях с точками.

В диаграмме выше вы можете выбрать количество точек. Если кривая острая, вам понадобится больше точек. Если кривая почти прямая линия, то вам, вероятно, понадобится меньше точек. Одно решение

• проверить, насколько изогнута кривая. Если она слишком изогнута, то разделить её на 2 кривые.

Часть разделения оказывается легкой. Если мы посмотрим на различные уровни интерполяции снова, точки P1, Q1, R1, КРАСНАЯ образуют одну кривую, а точки КРАСНАЯ, R2, Q3, P4 образуют другую для любого значения t. Другими словами, мы можем разделить кривую где угодно и получить 2 кривые, которые соответствуют оригиналу.

Вторая часть - решить, нужно ли разделять кривую или нет. Просматривая интернет, я нашел эту функцию, которая для данной кривой решает, насколько она плоская.

function flatness(points, offset) {
  const p1 = points[offset + 0];
  const p2 = points[offset + 1];
  const p3 = points[offset + 2];
  const p4 = points[offset + 3];

  let ux = 3 * p2[0] - 2 * p1[0] - p4[0]; ux *= ux;
  let uy = 3 * p2[1] - 2 * p1[1] - p4[1]; uy *= uy;
  let vx = 3 * p3[0] - 2 * p4[0] - p1[0]; vx *= vx;
  let vy = 3 * p3[1] - 2 * p4[1] - p1[1]; vy *= vy;

  if(ux < vx) {
    ux = vx;
  }

  if(uy < vy) {
    uy = vy;
  }

  return ux + uy;
}

Мы можем использовать это в нашей функции, которая получает точки для кривой. Сначала мы проверим, не слишком ли изогнута кривая. Если да, то разделим, если нет, то добавим точки.

function getPointsOnBezierCurveWithSplitting(points, offset, tolerance, newPoints) {
  const outPoints = newPoints || [];
  if (flatness(points, offset) < tolerance) {

    // просто добавляем конечные точки этой кривой
    outPoints.push(points[offset + 0]);
    outPoints.push(points[offset + 3]);

  } else {

    // разделяем
    const t = .5;
    const p1 = points[offset + 0];
    const p2 = points[offset + 1];
    const p3 = points[offset + 2];
    const p4 = points[offset + 3];

    const q1 = v2.lerp(p1, p2, t);
    const q2 = v2.lerp(p2, p3, t);
    const q3 = v2.lerp(p3, p4, t);

    const r1 = v2.lerp(q1, q2, t);
    const r2 = v2.lerp(q2, q3, t);

    const red = v2.lerp(r1, r2, t);

    // делаем первую половину
    getPointsOnBezierCurveWithSplitting([p1, q1, r1, red], 0, tolerance, outPoints);
    // делаем вторую половину
    getPointsOnBezierCurveWithSplitting([red, r2, q3, p4], 0, tolerance, outPoints);

  }
  return outPoints;
}

Этот алгоритм хорошо справляется с обеспечением достаточного количества точек, но он не так хорошо справляется с удалением ненужных точек.

Для этого мы обращаемся к алгоритму Рамера-Дугласа-Пекера, который я нашел в интернете.

В этом алгоритме мы берем список точек. Мы находим самую дальнюю точку от линии, образованной 2 конечными точками. Затем мы проверяем, находится ли эта точка дальше от линии, чем некоторое расстояние. Если она меньше этого расстояния, мы просто оставляем 2 конечные точки и отбрасываем остальные. В противном случае мы запускаем алгоритм снова, один раз с точками от начала до самой дальней точки и снова от самой дальней точки до конечной точки.

function simplifyPoints(points, start, end, epsilon, newPoints) {
  const outPoints = newPoints || [];

  // находим самую дальнюю точку от конечных точек
  const s = points[start];
  const e = points[end - 1];
  let maxDistSq = 0;
  let maxNdx = 1;
  for (let i = start + 1; i < end - 1; ++i) {
    const distSq = v2.distanceToSegmentSq(points[i], s, e);
    if (distSq > maxDistSq) {
      maxDistSq = distSq;
      maxNdx = i;
    }
  }

  // если эта точка слишком далеко
  if (Math.sqrt(maxDistSq) > epsilon) {

    // разделяем
    simplifyPoints(points, start, maxNdx + 1, epsilon, outPoints);
    simplifyPoints(points, maxNdx, end, epsilon, outPoints);

  } else {

    // добавляем 2 конечные точки
    outPoints.push(s, e);
  }

  return outPoints;
}

v2.distanceToSegmentSq - это функция, которая вычисляет квадрат расстояния от точки до отрезка линии. Мы используем квадрат расстояния, потому что его быстрее вычислять, чем фактическое расстояние. Поскольку нас интересует только то, какая точка самая дальняя, квадрат расстояния будет работать так же хорошо, как и фактическое расстояние.

Вот это в действии. Настройте расстояние, чтобы увидеть больше точек добавленных или удаленных.

Вернемся к нашей кегле. Мы могли бы попытаться расширить код выше в полноценный редактор. Ему нужно было бы уметь добавлять и удалять точки, блокировать и разблокировать контрольные точки. Ему понадобился бы откат и т.д… Но есть более простой способ. Мы можем просто использовать любой из основных редакторов, упомянутых выше. Я использовал этот онлайн редактор.

Вот SVG силуэт кегли, который я сделал.

Он сделан из 4 кривых Безье. Данные для этого пути выглядят так

<path fill="none" stroke-width="5" d="
   m44,434
   c18,-33 19,-66 15,-111
   c-4,-45 -37,-104 -39,-132
   c-2,-28 11,-51 16,-81
   c5,-30 3,-63 -36,-63
"/>

Интерпретируя эти данные, мы получаем эти точки.

        ___
44, 371,   |
62, 338,   | 1-я кривая
63, 305,___|__
59, 260,___|  |
55, 215,      | 2-я кривая
22, 156,______|__
20, 128,______|  |
18, 100,         | 3-я кривая
31,  77,_________|__
36,  47,_________|  |
41,  17,            | 4-я кривая
39, -16,            |
 0, -16,____________|

Теперь, когда у нас есть данные для кривых, нам нужно вычислить некоторые точки на них.

// получает точки по всем сегментам
function getPointsOnBezierCurves(points, tolerance) {
  const newPoints = [];
  const numSegments = (points.length - 1) / 3;
  for (let i = 0; i < numSegments; ++i) {
    const offset = i * 3;
    getPointsOnBezierCurveWithSplitting(points, offset, tolerance, newPoints);
  }
  return newPoints;
}

Мы бы вызвали simplifyPoints для результата.

Теперь нам нужно вращать их. Мы решаем, сколько делений сделать, для каждого деления вы используете матричную математику для вращения точек вокруг оси Y. Как только мы создали все точки, мы соединяем их треугольниками, используя индексы.

// вращает вокруг оси Y.
function lathePoints(points,
                     startAngle,   // угол для начала (т.е. 0)
                     endAngle,     // угол для окончания (т.е. Math.PI * 2)
                     numDivisions, // сколько четырехугольников сделать вокруг
                     capStart,     // true для закрытия начала
                     capEnd) {     // true для закрытия конца
  const positions = [];
  const texcoords = [];
  const indices = [];

  const vOffset = capStart ? 1 : 0;
  const pointsPerColumn = points.length + vOffset + (capEnd ? 1 : 0);
  const quadsDown = pointsPerColumn - 1;

  // генерируем точки
  for (let division = 0; division <= numDivisions; ++division) {
    const u = division / numDivisions;
    const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);
    const mat = m4.yRotation(angle);
    if (capStart) {
      // добавляем точку на оси Y в начале
      positions.push(0, points[0][1], 0);
      texcoords.push(u, 0);
    }
    points.forEach((p, ndx) => {
      const tp = m4.transformPoint(mat, [...p, 0]);
      positions.push(tp[0], tp[1], tp[2]);
      const v = (ndx + vOffset) / quadsDown;
      texcoords.push(u, v);
    });
    if (capEnd) {
      // добавляем точку на оси Y в конце
      positions.push(0, points[points.length - 1][1], 0);
      texcoords.push(u, 1);
    }
  }

  // генерируем индексы
  for (let division = 0; division < numDivisions; ++division) {
    const column1Offset = division * pointsPerColumn;
    const column2Offset = column1Offset + pointsPerColumn;
    for (let quad = 0; quad < quadsDown; ++quad) {
      indices.push(column1Offset + quad, column2Offset + quad, column1Offset + quad + 1);
      indices.push(column1Offset + quad + 1, column2Offset + quad, column2Offset + quad + 1);
    }
  }

  return {
    position: positions,
    texcoord: texcoords,
    indices: indices,
  };
}

Код выше генерирует позиции и текстурные координаты, затем генерирует индексы для создания треугольников из них. capStart и capEnd указывают, генерировать ли точки закрытия. Представьте, что мы делаем банку. Эти опции указывали бы, закрывать ли концы.

Используя наш упрощенный код, мы можем генерировать WebGL буферы с этими данными, как это

const tolerance = 0.15;
const distance = .4;
const divisions = 16;
const startAngle = 0;
const endAngle = Math.PI * 2;
const capStart = true;
const capEnd = true;

const tempPoints = getPointsOnBezierCurves(curvePoints, tolerance);
const points = simplifyPoints(tempPoints, 0, tempPoints.length, distance);
const arrays = lathePoints(points, startAngle, endAngle, divisions, capStart, capEnd);
const extents = getExtents(arrays.position);
if (!bufferInfo) {
  bufferInfo = webglUtils.createBufferInfoFromArrays(gl, arrays);

Вот пример

Поиграйте с ползунками, чтобы увидеть, как они влияют на результат.

Однако есть проблема. Включите треугольники, и вы увидите, что текстура не применяется равномерно. Это потому, что мы основали координату v на индексе точек на линии. Если бы они были равномерно распределены, это могло бы работать. Но они не равномерно распределены, поэтому нам нужно сделать что-то другое.

Мы можем пройти по точкам и вычислить общую длину кривой и расстояние каждой точки на этой кривой. Затем мы можем разделить на длину и получить лучшее значение для v.

// вращает вокруг оси Y.
function lathePoints(points,
                     startAngle,   // угол для начала (т.е. 0)
                     endAngle,     // угол для окончания (т.е. Math.PI * 2)
                     numDivisions, // сколько четырехугольников сделать вокруг
                     capStart,     // true для закрытия верха
                     capEnd) {     // true для закрытия низа
  const positions = [];
  const texcoords = [];
  const indices = [];

  const vOffset = capStart ? 1 : 0;
  const pointsPerColumn = points.length + vOffset + (capEnd ? 1 : 0);
  const quadsDown = pointsPerColumn - 1;

+  // генерируем v координаты
+  let vcoords = [];
+
+  // сначала вычисляем длину точек
+  let length = 0;
+  for (let i = 0; i < points.length - 1; ++i) {
+    vcoords.push(length);
+    length += v2.distance(points[i], points[i + 1]);
+  }
+  vcoords.push(length);  // последняя точка
+
+  // теперь делим каждую на общую длину;
+  vcoords = vcoords.map(v => v / length);

  // генерируем точки
  for (let division = 0; division <= numDivisions; ++division) {
    const u = division / numDivisions;
    const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);
    const mat = m4.yRotation(angle);
    if (capStart) {
      // добавляем точку на оси Y в начале
      positions.push(0, points[0][1], 0);
      texcoords.push(u, 0);
    }
    points.forEach((p, ndx) => {
      const tp = m4.transformPoint(mat, [...p, 0]);
      positions.push(tp[0], tp[1], tp[2]);
*      texcoords.push(u, vcoords[ndx]);
    });
    if (capEnd) {
      // добавляем точку на оси Y в конце
      positions.push(0, points[points.length - 1][1], 0);
      texcoords.push(u, 1);
    }
  }

  // генерируем индексы
  for (let division = 0; division < numDivisions; ++division) {
    const column1Offset = division * pointsPerColumn;
    const column2Offset = column1Offset + pointsPerColumn;
    for (let quad = 0; quad < quadsDown; ++quad) {
      indices.push(column1Offset + quad, column1Offset + quad + 1, column2Offset + quad);
      indices.push(column1Offset + quad + 1, column2Offset + quad + 1, column2Offset + quad);
    }
  }

  return {
    position: positions,
    texcoord: texcoords,
    indices: indices,
  };
}

И вот результат

Эти координаты текстуры все еще не идеальны. Мы не решили, что делать для крышек. Это еще одна причина, почему вы должны просто использовать программу моделирования. Мы могли бы придумать разные идеи о том, как вычислять uv координаты для крышек, но они, вероятно, не будут особенно полезными. Если вы погуглите “UV map a barrel”, вы увидите, что получение идеальных UV координат - это не столько математическая проблема, сколько проблема ввода данных, и вам нужны хорошие инструменты для ввода этих данных.

Есть еще одна вещь, которую мы должны сделать, и это добавить нормали.

Мы могли бы вычислить нормаль для каждой точки на кривой. Фактически, если вы вернетесь к примерам на этой странице, вы можете увидеть, что линия, образованная R1 и R2, является касательной к кривой.

Нормаль перпендикулярна касательной, поэтому было бы легко использовать касательные для генерации нормалей.

Но давайте представим, что мы хотели сделать подсвечник с силуэтом, как этот

Есть много гладких областей, но также много острых углов. Как мы решаем, какие нормали использовать? Хуже того, когда мы хотим острый край, нам нужны дополнительные вершины. Потому что вершины имеют как позицию, так и нормаль, если нам нужна другая нормаль для чего-то в той же позиции, то нам нужна другая вершина. Вот почему, если мы делаем куб, нам фактически нужно как минимум 24 вершины. Хотя у куба только 8 углов, каждой грани куба нужны разные нормали в этих углах.

При генерации куба легко просто генерировать правильные нормали, но для более сложной формы нет простого способа решить.

Все программы моделирования имеют различные опции для генерации нормалей. Обычный способ - для каждой отдельной вершины они усредняют нормали всех многоугольников, которые используют эту вершину. За исключением того, что они позволяют пользователю выбрать некоторый максимальный угол. Если угол между одним многоугольником, используемым вершиной, больше этого максимального угла, то они генерируют новую вершину.

Давайте сделаем это.

function generateNormals(arrays, maxAngle) {
  const positions = arrays.position;
  const texcoords = arrays.texcoord;

  // сначала вычисляем нормаль каждого лица
  let getNextIndex = makeIndiceIterator(arrays);
  const numFaceVerts = getNextIndex.numElements;
  const numVerts = arrays.position.length;
  const numFaces = numFaceVerts / 3;
  const faceNormals = [];

  // Вычисляем нормаль для каждого лица.
  // Делая это, создаем новую вершину для каждой вершины лица
  for (let i = 0; i < numFaces; ++i) {
    const n1 = getNextIndex() * 3;
    const n2 = getNextIndex() * 3;
    const n3 = getNextIndex() * 3;

    const v1 = positions.slice(n1, n1 + 3);
    const v2 = positions.slice(n2, n2 + 3);
    const v3 = positions.slice(n3, n3 + 3);

    faceNormals.push(m4.normalize(m4.cross(m4.subtractVectors(v1, v2), m4.subtractVectors(v3, v2))));
  }

  let tempVerts = {};
  let tempVertNdx = 0;

  // это предполагает, что позиции вершин точно совпадают

  function getVertIndex(x, y, z) {

    const vertId = x + "," + y + "," + z;
    const ndx = tempVerts[vertId];
    if (ndx !== undefined) {
      return ndx;
    }
    const newNdx = tempVertNdx++;
    tempVerts[vertId] = newNdx;
    return newNdx;
  }

  // Нам нужно выяснить общие вершины.
  // Это не так просто, как смотреть на лица (треугольники),
  // потому что, например, если у нас есть стандартный цилиндр
  //
  //
  //      3-4
  //     /   \
  //    2     5   Смотрим вниз на цилиндр, начиная с S
  //    |     |   и идя вокруг к E, E и S не являются
  //    1     6   той же вершиной в данных, которые у нас есть,
  //     \   /    поскольку они не используют общие UV координаты.
  //      S/E
  //
  // вершины в начале и конце не используют общие вершины,
  // поскольку у них разные UV, но если вы не считаете
  // их общими вершинами, они получат неправильные нормали

  const vertIndices = [];
  for (let i = 0; i < numVerts; ++i) {
    const offset = i * 3;
    const vert = positions.slice(offset, offset + 3);
    vertIndices.push(getVertIndex(vert));
  }

  // проходим через каждую вершину и записываем, на каких лицах она находится
  const vertFaces = [];
  getNextIndex.reset();
  for (let i = 0; i < numFaces; ++i) {
    for (let j = 0; j < 3; ++j) {
      const ndx = getNextIndex();
      const sharedNdx = vertIndices[ndx];
      let faces = vertFaces[sharedNdx];
      if (!faces) {
        faces = [];
        vertFaces[sharedNdx] = faces;
      }
      faces.push(i);
    }
  }

  // теперь проходим через каждое лицо и вычисляем нормали для каждой
  // вершины лица. Включаем только лица, которые не отличаются больше чем
  // на maxAngle. Добавляем результат в массивы newPositions,
  // newTexcoords и newNormals, отбрасывая любые вершины, которые
  // одинаковы.
  tempVerts = {};
  tempVertNdx = 0;
  const newPositions = [];
  const newTexcoords = [];
  const newNormals = [];

  function getNewVertIndex(x, y, z, nx, ny, nz, u, v) {
    const vertId =
        x + "," + y + "," + z + "," +
        nx + "," + ny + "," + nz + "," +
        u + "," + v;

    const ndx = tempVerts[vertId];
    if (ndx !== undefined) {
      return ndx;
    }
    const newNdx = tempVertNdx++;
    tempVerts[vertId] = newNdx;
    newPositions.push(x, y, z);
    newNormals.push(nx, ny, nz);
    newTexcoords.push(u, v);
    return newNdx;
  }

  const newVertIndices = [];

  getNextIndex.reset();
  const maxAngleCos = Math.cos(maxAngle);
  // для каждого лица
  for (let i = 0; i < numFaces; ++i) {
    // получаем нормаль для этого лица
    const thisFaceNormal = faceNormals[i];
    // для каждой вершины на лице
    for (let j = 0; j < 3; ++j) {
      const ndx = getNextIndex();
      const sharedNdx = vertIndices[ndx];
      const faces = vertFaces[sharedNdx];
      const norm = [0, 0, 0];
      faces.forEach(faceNdx => {
        // это лицо смотрит в том же направлении
        const otherFaceNormal = faceNormals[faceNdx];
        const dot = m4.dot(thisFaceNormal, otherFaceNormal);
        if (dot > maxAngleCos) {
          m4.addVectors(norm, otherFaceNormal, norm);
        }
      });
      m4.normalize(norm, norm);
      const poffset = ndx * 3;
      const toffset = ndx * 2;
      newVertIndices.push(getNewVertIndex(
          positions[poffset + 0], positions[poffset + 1], positions[poffset + 2],
          norm[0], norm[1], norm[2],
          texcoords[toffset + 0], texcoords[toffset + 1]));
    }
  }

  return {
    position: newPositions,
    texcoord: newTexcoords,
    normal: newNormals,
    indices: newVertIndices,
  };

}

function makeIndexedIndicesFn(arrays) {
  const indices = arrays.indices;
  let ndx = 0;
  const fn = function() {
    return indices[ndx++];
  };
  fn.reset = function() {
    ndx = 0;
  };
  fn.numElements = indices.length;
  return fn;
}

function makeUnindexedIndicesFn(arrays) {
  let ndx = 0;
  const fn = function() {
    return ndx++;
  };
  fn.reset = function() {
    ndx = 0;
  }
  fn.numElements = arrays.positions.length / 3;
  return fn;
}

function makeIndiceIterator(arrays) {
  return arrays.indices
      ? makeIndexedIndicesFn(arrays)
      : makeUnindexedIndicesFn(arrays);
}

В коде выше сначала мы генерируем нормали для каждого лица (каждого треугольника) из исходных точек. Затем мы генерируем набор индексов вершин, чтобы найти точки, которые одинаковы. Это потому, что когда мы вращали точки, первая точка и последняя точка должны совпадать, но у них разные UV координаты, поэтому они не являются одной и той же точкой. Для вычисления нормалей вершин нам нужно, чтобы они считались одной и той же точкой.

После того, как это сделано, для каждой вершины мы составляем список всех лиц, которые она использует.

Наконец, мы усредняем нормали всех лиц, которые использует каждая вершина, исключая те, которые отличаются больше чем на maxAngle, и генерируем новый набор вершин.

Вот результат

Обратите внимание, что мы получаем острые края там, где мы их хотим. Сделайте maxAngle больше, и вы увидите, как эти края сглаживаются, когда соседние лица начинают включаться в вычисления нормалей. Также попробуйте настроить divisions на что-то вроде 5 или 6, затем настройте maxAngle, пока края вокруг не станут жесткими, но части, которые вы хотите сгладить, остались сглаженными. Вы также можете установить mode на lit, чтобы увидеть, как объект будет выглядеть с освещением, причина, по которой нам нужны нормали.

Итак, чему мы научились?

Мы научились, что если вы хотите создавать 3D данные, ИСПОЛЬЗУЙТЕ ПАКЕТ 3D МОДЕЛИРОВАНИЯ!!! 😝

Чтобы сделать что-то действительно полезное, вам, вероятно, понадобится настоящий UV редактор. Работа с крышками также является чем-то, с чем поможет 3D редактор. Вместо использования ограниченного набора опций при токарной обработке, вы бы использовали другие функции редактора для добавления крышек и генерации более простых UV для крышек. 3D редакторы также поддерживают выдавливание граней и выдавливание вдоль пути, которые, если вы посмотрите, должно быть довольно очевидно, как они работают, основываясь на примере токарной обработки выше.

Ссылки

Я хотел упомянуть, что не смог бы сделать это без этой потрясающей страницы о кривых Безье.

Что делает здесь оператор модуло?

Если вы внимательно посмотрите на функцию lathePoints, вы увидите этот модуло при вычислении угла.

for (let division = 0; division <= numDivisions; ++division) {
  const u = division / numDivisions;
*  const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);

Почему он там?

Когда мы вращаем точки полностью вокруг круга, мы действительно хотим, чтобы первая и последняя точки совпадали. Math.sin(0) и Math.sin(Math.PI * 2) должны совпадать, но математика с плавающей точкой на компьютере не идеальна, и хотя они достаточно близки в общем, они не являются на самом деле 100% равными.

Это важно, когда мы пытаемся вычислить нормали. Мы хотим знать все лица, которые использует вершина. Мы вычисляем это, сравнивая вершины. Если 2 вершины равны, мы предполагаем, что они являются одной и той же вершиной. К сожалению, поскольку Math.sin(0) и Math.sin(Math.PI * 2) не равны, они не будут считаться одной и той же вершиной. Это означает, что при вычислении нормалей они не будут учитывать все лица, и их нормали будут неправильными.

Вот результат, когда это происходит

Как вы можете видеть, есть шов, где вершины не считаются общими, потому что они не являются 100% совпадением

Моя первая мысль была, что я должен изменить мое решение так, чтобы когда я проверяю совпадающие вершины, я проверял, находятся ли они в пределах некоторого расстояния. Если да, то они одна и та же вершина. Что-то вроде этого.

const epsilon = 0.0001;
const tempVerts = [];
function getVertIndex(position) {
  if (tempVerts.length) {
    // найти ближайшую существующую вершину
    let closestNdx = 0;
    let closestDistSq = v2.distanceSq(position, tempVerts[0]);
    for (let i = 1; i < tempVerts.length; ++i) {
      let distSq = v2.distanceSq(position, tempVerts[i]);
      if (distSq < closestDistSq) {
        closestDistSq = distSq;
        closestNdx = i;
      }
    }
    // была ли ближайшая вершина достаточно близко?
    if (closestDistSq < epsilon) {
      // да, поэтому просто возвращаем индекс этой вершины.
      return closestNdx;
    }
  }
  // нет совпадения, добавляем вершину как новую вершину и возвращаем её индекс.
  tempVerts.push(position);
  return tempVerts.length - 1;
}

Это сработало! Это убрало шов. К сожалению, это заняло несколько секунд для выполнения и сделало интерфейс непригодным для использования. Это потому, что это решение O^2. Если вы сдвинете ползунки для наибольшего количества вершин (distance/divisions) в примере выше, вы можете сгенерировать ~114000 вершин. Для O^2 это до 12 миллиардов итераций, которые должны произойти.

Я искал в интернете простое решение. Я не нашел. Я думал о том, чтобы поместить все точки в [октодерево](https://en.wikipedia.org/wiki/Octree), чтобы сделать поиск совпадающих точек быстрее, но это кажется слишком много для этой статьи.

Именно тогда я понял, что если единственная проблема - конечные точки, возможно, я мог бы добавить модуло к математике, чтобы точки были на самом деле одинаковыми. Исходный код был таким

  const angle = lerp(startAngle, endAngle, u);

А новый код таким

  const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);

Из-за модуло angle, когда endAngle равен Math.PI * 2, становится 0 и поэтому он такой же, как начало. Шов исчез. Проблема решена!

Тем не менее, даже с изменением, если вы установите distance на 0.001 и divisions на 60, это занимает почти секунду на моей машине для пересчета сетки. Хотя могут быть способы оптимизировать это, я думаю, что суть в понимании, что генерация сложных сеток - это вообще медленная операция. Это всего лишь один пример того, почему 3D игра может работать на 60fps, но 3D пакет моделирования часто работает на очень медленных частотах кадров.

const mat = m4.yRotation(angle);
...
points.forEach((p, ndx) => {
  const tp = m4.transformPoint(mat, [...p, 0]);
  ...

const s = Math.sin(angle);
const c = Math.cos(angle);
...
points.forEach((p, ndx) => {
  const x = p[0];
  const y = p[1];
  const z = p[2];
  const tp = [
    x * c - z * s,
    y,
    x * s + z * c,
  ];
  ...

   const mat = m4.axisRotation(userSuppliedAxis, angle);