Этот пост является продолжением серии постов о WebGL. Первый начался с основ, а предыдущий был о трансляции геометрии.

Я сразу признаюсь, что не знаю, будет ли то, как я объясняю это, иметь смысл, но черт с ним, стоит попробовать.

Сначала я хочу познакомить вас с тем, что называется “единичной окружностью”. Если вы помните математику средней школы (не засыпайте на мне!) окружность имеет радиус. Радиус окружности - это расстояние от центра окружности до края. Единичная окружность - это окружность с радиусом 1.0.

Вот единичная окружность.

Обратите внимание, как вы перетаскиваете синюю ручку вокруг окружности, позиции X и Y изменяются. Они представляют позицию этой точки на окружности. Вверху Y равен 1, а X равен 0. Справа X равен 1, а Y равен 0.

Если вы помните из базовой математики 3-го класса, если вы умножаете что-то на 1, оно остается тем же. Так что 123 * 1 = 123. Довольно просто, верно? Ну, единичная окружность, окружность с радиусом 1.0, также является формой 1. Это вращающаяся 1. Так что вы можете умножить что-то на эту единичную окружность, и в некотором смысле это как умножение на 1, за исключением того, что происходит магия и вещи вращаются.

Мы возьмем эти значения X и Y из любой точки на единичной окружности и умножим нашу геометрию на них из нашего предыдущего примера.

Вот обновления нашего шейдера.

#version 300 es

in vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Вращаем позицию
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Добавляем трансляцию.
  vec2 position = rotatedPosition + u_translation;

  // конвертируем позицию из пикселей в 0.0 до 1.0
  vec2 zeroToOne = position / u_resolution;

  // конвертируем из 0->1 в 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // конвертируем из 0->2 в -1->+1 (clip space)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
}

И мы обновляем JavaScript, чтобы мы могли передать эти 2 значения.

  ...

  var rotationLocation = gl.getUniformLocation(program, "u_rotation");

  ...

  var rotation = [0, 1];

  ...

  // Рисуем сцену.
  function drawScene() {
    webglUtils.resizeCanvasToDisplaySize(gl.canvas);

    // Говорим WebGL, как конвертировать из clip space в пиксели
    gl.viewport(0, 0, gl.canvas.width, gl.canvas.height);

    // Очищаем canvas
    gl.clearColor(0, 0, 0, 0);
    gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

    // Говорим использовать нашу программу (пару шейдеров)
    gl.useProgram(program);

    // Привязываем набор атрибутов/буферов, который мы хотим.
    gl.bindVertexArray(vao);

    // Передаем разрешение canvas, чтобы мы могли конвертировать из
    // пикселей в clip space в шейдере
    gl.uniform2f(resolutionUniformLocation, gl.canvas.width, gl.canvas.height);

    // Устанавливаем цвет.
    gl.uniform4fv(colorLocation, color);

    // Устанавливаем трансляцию.
    gl.uniform2fv(translationLocation, translation);

    // Устанавливаем вращение.
    gl.uniform2fv(rotationLocation, rotation);

    // Рисуем прямоугольник.
    var primitiveType = gl.TRIANGLES;
    var offset = 0;
    var count = 18;
    gl.drawArrays(primitiveType, offset, count);
  }

И вот результат. Перетащите ручку на окружности, чтобы вращать, или слайдеры, чтобы трансформировать.

Почему это работает? Ну, посмотрите на математику.

    rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
    rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Допустим, у вас есть прямоугольник, и вы хотите его вращать. Прежде чем вы начнете его вращать, верхний правый угол находится в точке 3.0, 9.0. Давайте выберем точку на единичной окружности на 30 градусов по часовой стрелке от 12 часов.

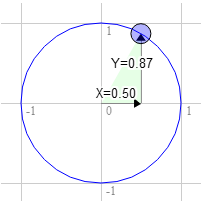
Позиция на окружности там 0.50 и 0.87

   3.0 * 0.87 + 9.0 * 0.50 = 7.1
   9.0 * 0.87 - 3.0 * 0.50 = 6.3

Это именно там, где нам нужно

То же самое для 60 градусов по часовой стрелке

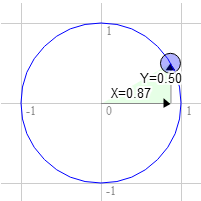
Позиция на окружности там 0.87 и 0.50

   3.0 * 0.50 + 9.0 * 0.87 = 9.3
   9.0 * 0.50 - 3.0 * 0.87 = 1.9

Вы можете видеть, что когда мы вращаем эту точку по часовой стрелке вправо, значение X становится больше, а Y становится меньше. Если бы мы продолжали за 90 градусов, X снова начал бы становиться меньше, а Y начал бы становиться больше. Этот паттерн дает нам вращение.

Есть другое название для точек на единичной окружности. Они называются синус и косинус. Так что для любого заданного угла мы можем просто посмотреть синус и косинус, как это.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

Если вы скопируете и вставите код в консоль JavaScript и напишете printSineAndCosignForAngle(30), вы увидите, что он выводит s = 0.49 c = 0.87 (примечание: я округлил числа.)

Если вы все это сложите вместе, вы можете вращать вашу геометрию на любой угол, который вы желаете. Просто установите вращение на синус и косинус угла, на который вы хотите вращать.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

Вот версия, которая просто имеет настройку угла. Перетащите слайдеры, чтобы трансформировать или вращать.

Я надеюсь, что это имело некоторый смысл. Следующий более простой. Масштабирование.