Этот пост является продолжением серии постов о WebGL. Первый начался с основ и предыдущий был о 3D Основы. Если вы не читали их, пожалуйста, просмотрите их сначала.

В последнем посте мы рассмотрели, как делать 3D, но этот 3D не имел никакой перспективы. Он использовал то, что называется “ортографическим” видом, который имеет свои применения, но это обычно не то, что люди хотят, когда говорят “3D”.

Вместо этого нам нужно добавить перспективу. Что такое перспектива? Это в основном особенность, что вещи, которые находятся дальше, выглядят меньше.

Глядя на пример выше, мы видим, что вещи дальше рисуются меньше. Учитывая наш текущий пример, один простой способ сделать так, чтобы вещи, которые находятся дальше, выглядели меньше, было бы разделить clip space X и Y на Z.

Думайте об этом так: Если у вас есть линия от (10, 15) до (20,15), она длиной 10 единиц. В нашем текущем примере она была бы нарисована длиной 10 пикселей. Но если мы разделим на Z, то, например, если Z равен 1

10 / 1 = 10
20 / 1 = 20
abs(10-20) = 10

она была бы длиной 10 пикселей. Если Z равен 2, она была бы

10 / 2 = 5
20 / 2 = 10
abs(5 - 10) = 5

длиной 5 пикселей. При Z = 3 она была бы

10 / 3 = 3.333
20 / 3 = 6.666
abs(3.333 - 6.666) = 3.333

Вы можете видеть, что по мере увеличения Z, по мере того, как он становится дальше, мы в конечном итоге рисуем его меньше. Если мы разделим в clip space, мы можем получить лучшие результаты, потому что Z будет меньшим числом (-1 до +1). Если мы добавим fudgeFactor, чтобы умножить Z перед тем, как мы разделим, мы можем настроить, насколько меньше вещи становятся для данного расстояния.

Давайте попробуем это. Сначала давайте изменим вершинный шейдер, чтобы разделить на Z после того, как мы умножили его на наш “fudgeFactor”.

...
+uniform float u_fudgeFactor;
...
void main() {
  // Умножаем позицию на матрицу.
*  vec4 position = u_matrix * a_position;

  // Настраиваем z для деления на
+  float zToDivideBy = 1.0 + position.z * u_fudgeFactor;

  // Делим x и y на z.
*  gl_Position = vec4(position.xy / zToDivideBy, position.zw);
}

Обратите внимание, поскольку Z в clip space идет от -1 до +1, я добавил 1, чтобы получить zToDivideBy, чтобы он шел от 0 до +2 * fudgeFactor

Нам также нужно обновить код, чтобы позволить нам установить fudgeFactor.

  ...
+  var fudgeLocation = gl.getUniformLocation(program, "u_fudgeFactor");

  ...
+  var fudgeFactor = 1;
  ...
  function drawScene() {
    ...
+    // Устанавливаем fudgeFactor
+    gl.uniform1f(fudgeLocation, fudgeFactor);

    // Рисуем геометрию.
    gl.drawArrays(gl.TRIANGLES, 0, 16 * 6);

И вот результат.

Если это не ясно, перетащите слайдер “fudgeFactor” с 1.0 на 0.0, чтобы увидеть, как вещи выглядели раньше, прежде чем мы добавили наш код деления на Z.

Оказывается, WebGL берет значение x,y,z,w, которое мы присваиваем gl_Position в нашем вершинном шейдере, и автоматически делит его на w.

Мы можем доказать это очень легко, изменив шейдер и вместо того, чтобы делать деление сами, поместить zToDivideBy в gl_Position.w.

...
uniform float u_fudgeFactor;
...
void main() {
  // Умножаем позицию на матрицу.
  vec4 position = u_matrix * a_position;

  // Настраиваем z для деления на
  float zToDivideBy = 1.0 + position.z * u_fudgeFactor;

  // Делим x, y и z на zToDivideBy
  gl_Position = vec4(position.xyz,  zToDivideBy);
}

и посмотреть, как это точно то же самое.

Почему тот факт, что WebGL автоматически делит на W, полезен? Потому что теперь, используя больше матричной магии, мы можем просто использовать еще одну матрицу, чтобы скопировать z в w.

Матрица, как эта

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 1,
0, 0, 0, 0,

скопирует z в w. Вы можете смотреть на каждый из этих столбцов как

x_out = x_in * 1 +
        y_in * 0 +
        z_in * 0 +
        w_in * 0 ;
y_out = x_in * 0 +
y_in * 1 +
z_in * 0 +
w_in * 0 ;
z_out = x_in * 0 +
y_in * 0 +
z_in * 1 +
w_in * 0 ;
w_out = x_in * 0 +
y_in * 0 +
z_in * 1 +
w_in * 0 ;

что при упрощении есть

x_out = x_in;
y_out = y_in;
z_out = z_in;
w_out = z_in;

Мы можем добавить плюс 1, который у нас был раньше, с этой матрицей, поскольку мы знаем, что w_in всегда 1.0.

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 1,
0, 0, 0, 1,

это изменит вычисление W на

w_out = x_in * 0 +
        y_in * 0 +
        z_in * 1 +
        w_in * 1 ;

и поскольку мы знаем, что w_in = 1.0, то это действительно

w_out = z_in + 1;

Наконец, мы можем вернуть наш fudgeFactor, если матрица такая

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, fudgeFactor,
0, 0, 0, 1,

что означает

w_out = x_in * 0 +
        y_in * 0 +
        z_in * fudgeFactor +
        w_in * 1 ;

и упрощенно это

w_out = z_in * fudgeFactor + 1;

Итак, давайте снова изменим программу, чтобы просто использовать матрицы.

Сначала давайте вернем вершинный шейдер. Он снова простой

uniform mat4 u_matrix;

void main() {
  // Умножаем позицию на матрицу.
  gl_Position = u_matrix * a_position;
  ...
}

Далее давайте сделаем функцию для создания нашей матрицы Z → W.

function makeZToWMatrix(fudgeFactor) {
  return [
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, fudgeFactor,
    0, 0, 0, 1,
  ];
}

и мы изменим код, чтобы использовать ее.

    ...

    // Вычисляем матрицу
+    var matrix = makeZToWMatrix(fudgeFactor);
*    matrix = m4.multiply(matrix, m4.projection(gl.canvas.clientWidth, gl.canvas.clientHeight, 400));
    matrix = m4.translate(matrix, translation[0], translation[1], translation[2]);
    matrix = m4.xRotate(matrix, rotation[0]);
    matrix = m4.yRotate(matrix, rotation[1]);
    matrix = m4.zRotate(matrix, rotation[2]);
    matrix = m4.scale(matrix, scale[0], scale[1], scale[2]);

    ...

и обратите внимание, снова, это точно то же самое.

Все это было в основном просто чтобы показать вам, что деление на Z дает нам перспективу и что WebGL удобно делает это деление на Z для нас.

Но все еще есть некоторые проблемы. Например, если вы установите Z примерно на -100, вы увидите что-то вроде анимации ниже

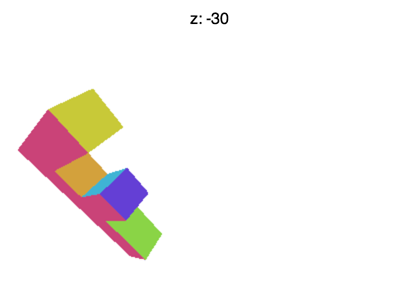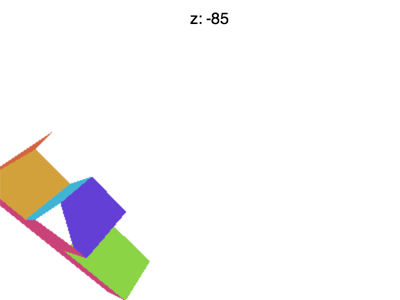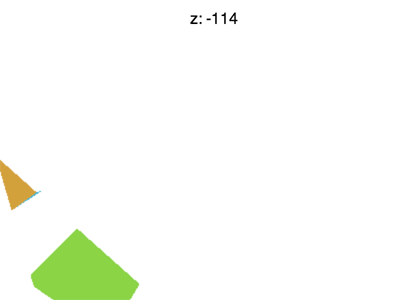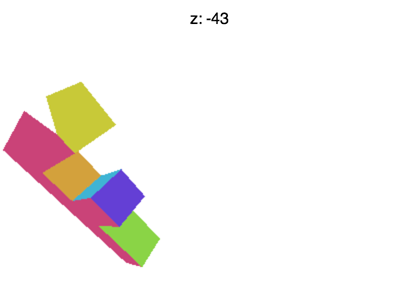
Что происходит? Почему F исчезает рано? Так же, как WebGL обрезает X и Y до значений между +1 и -1, он также обрезает Z. То, что мы видим здесь, это где Z < -1.

Я мог бы вдаваться в детали математики, чтобы исправить это, но вы можете вывести это так же, как мы делали 2D проекцию. Нам нужно взять Z, добавить некоторое количество и масштабировать некоторое количество, и мы можем сделать любой диапазон, который мы хотим, перемаппированным в -1 до +1.

Крутая вещь в том, что все эти шаги могут быть сделаны в 1 матрице. Еще лучше, вместо fudgeFactor мы решим на fieldOfView и вычислим правильные значения, чтобы это произошло.

Вот функция для построения матрицы.

var m4 = {
  perspective: function(fieldOfViewInRadians, aspect, near, far) {
    var f = Math.tan(Math.PI * 0.5 - 0.5 * fieldOfViewInRadians);
    var rangeInv = 1.0 / (near - far);

    return [
      f / aspect, 0, 0, 0,
      0, f, 0, 0,
      0, 0, (near + far) * rangeInv, -1,
      0, 0, near * far * rangeInv * 2, 0
    ];
  },

  ...

Эта матрица сделает все наши преобразования для нас. Она настроит единицы так, чтобы они были в clip space, она сделает математику так, чтобы мы могли выбрать поле зрения по углу, и она позволит нам выбрать наше Z-обрезающее пространство. Она предполагает, что есть глаз или камера в начале координат (0, 0, 0), и учитывая zNear и fieldOfView, она вычисляет, что потребуется, чтобы вещи на zNear оказались на Z = -1, а вещи на zNear, которые составляют половину fieldOfView выше или ниже центра, оказались с Y = -1 и Y = 1 соответственно. Она вычисляет, что использовать для X, просто умножая на переданный aspect. Мы обычно устанавливаем это в width / height области отображения. Наконец, она выясняет, насколько масштабировать вещи в Z, чтобы вещи на zFar оказались на Z = 1.

Вот диаграмма матрицы в действии.

Эта форма, которая выглядит как 4-сторонний конус, в котором вращаются кубы, называется “усеченной пирамидой”. Матрица берет пространство внутри усеченной пирамиды и преобразует это в clip space. zNear определяет, где вещи будут обрезаны спереди, а zFar определяет, где вещи обрезаются сзади. Установите zNear на 23, и вы увидите, как передняя часть вращающихся кубов обрезается. Установите zFar на 24, и вы увидите, как задняя часть кубов обрезается.

Остается только одна проблема. Эта матрица предполагает, что есть зритель в 0,0,0, и она предполагает, что он смотрит в отрицательном направлении Z и что положительный Y вверх. Наши матрицы до этого момента делали вещи по-другому.

Чтобы заставить это появиться, нам нужно переместить это внутрь усеченной пирамиды. Мы можем сделать это, переместив наш F. Мы рисовали в (45, 150, 0). Давайте переместим его в (-150, 0, -360) и давайте установим вращение на что-то, что заставляет его появиться правой стороной вверх.

Теперь, чтобы использовать это, нам просто нужно заменить наш старый вызов m4.projection на вызов m4.perspective

   var aspect = gl.canvas.clientWidth / gl.canvas.clientHeight;
   var zNear = 1;
   var zFar = 2000;
   var matrix = m4.perspective(fieldOfViewRadians, aspect, zNear, zFar);
   matrix = m4.translate(matrix, translation[0], translation[1], translation[2]);
   matrix = m4.xRotate(matrix, rotation[0]);
   matrix = m4.yRotate(matrix, rotation[1]);
   matrix = m4.zRotate(matrix, rotation[2]);
   matrix = m4.scale(matrix, scale[0], scale[1], scale[2]);

И вот это.

Мы вернулись к простому умножению матрицы, и мы получаем как поле зрения, так и возможность выбрать наше Z пространство. Мы не закончили, но эта статья становится слишком длинной. Далее камеры.

Почему мы переместили F так далеко в Z (-360)?

В других примерах у нас был F в (45, 150, 0), но в последнем примере он был перемещен в (-150, 0, -360). Почему его нужно было переместить так далеко?

Причина в том, что до этого последнего примера наша функция m4.projection делала проекцию из пикселей в clip space. Это означает, что область, которую мы отображали, представляла 400x300 пикселей. Использование ‘пикселей’ действительно не имеет смысла в 3D.

Другими словами, если бы мы попытались нарисовать с F в 0,0,0 и не повернутым, мы бы получили это

F имеет свой верхний левый передний угол в начале координат. Проекция смотрит в отрицательном направлении Z, но наш F построен в положительном Z. Проекция имеет положительный Y вверх, но наш F построен с положительным Z вниз.

Наша новая проекция видит только то, что в синей усеченной пирамиде. С -zNear = 1 и с полем зрения 60 градусов, то при Z = -1 усеченная пирамида только 1.154 единицы высотой и 1.154 * aspect единиц шириной. При Z = -2000 (-zFar) она 2309 единиц высотой. Поскольку наш F размером 150 единиц, а вид может видеть только 1.154 единицы, когда что-то находится на -zNear, нам нужно переместить это довольно далеко от начала координат, чтобы увидеть все это.

Перемещение его на -360 единиц в Z перемещает его внутрь усеченной пирамиды. Мы также повернули его, чтобы он был правой стороной вверх.

не в масштабе