Esse tópico é uma continuação de uma série de posts sobre a WebGL. O primeiro iniciou com os fundamentos e o anterior foi sobre translação de geometrias.

Eu tenho que admitir, agora mesmo, que eu não faço ideia se a maneira como eu explico irá fazer sentido, mas não importa, eu posso tentar.

Primeiro, eu quero lhe introduzir ao que é chamado de “círculo unitário”. Se você lembra da matemática do ensino médio (não vá dormir, ein!), um círculo possui um raio. O raio de um círculo é a distãncia do centro do círculo até sua extremidade. Um círculo unitário é, na verdade, um círculo com o raio de 1.0.

Aqui está um exemplo de um círculo unitário.

Observe que, de acordo com o que você arrasta a alça azul em torno do círculo, as posições X e Y mudam. Eles representam a posição desse ponto no círculo. Na parte superior, Y é 1 e X é 0. Na direita, X é 1 e Y é 0.

Se você se lembra da matemática básica de 3ª série, se você multiplicar algo por 1, o valor multiplicado continua igual. Então 123 * 1 = 123. Muito básico, certo? Bem, um círculo unitário, um círculo com um raio de 1.0, também é uma forma de 1. É um 1 que está rotacionando. Então, você pode multiplicar algo por este círculo unitário e, de certa forma, é como multiplicar por 1, exceto que a magia acontece e as coisas rotacionam.

Nós vamos pegar os valores de X e Y, de qualquer ponto no círculo unitário e, vamos multiplicar nossa geometria de acordo com nosso exemplo anterior.

Aqui vão alguns updates para o nosso shader.

#version 300 es

in vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
+uniform vec2 u_rotation;

void main() {
+ // Rotate the position
+  vec2 rotatedPosition = vec2(
+     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
+     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
* vec2 position = rotatedPosition + u_translation;

...

E também atualizamos o JavaScript para que possámos passar os dois valores.

  ...

+  var rotationLocation = gl.getUniformLocation(program, "u_rotation");

  ...

+  var rotation = [0, 1];

  ...

  // Draw the scene.
  function drawScene() {
    webglUtils.resizeCanvasToDisplaySize(gl.canvas);

    // Tell WebGL how to convert from clip space to pixels
    gl.viewport(0, 0, gl.canvas.width, gl.canvas.height);

    // Clear the canvas
    gl.clearColor(0, 0, 0, 0);
    gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

    // Tell it to use our program (pair of shaders)
    gl.useProgram(program);

    // Bind the attribute/buffer set we want.
    gl.bindVertexArray(vao);

    // Pass in the canvas resolution so we can convert from
    // pixels to clipspace in the shader
    gl.uniform2f(resolutionUniformLocation, gl.canvas.width, gl.canvas.height);

    // Set the color.
    gl.uniform4fv(colorLocation, color);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

+    // Set the rotation.
+    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    var primitiveType = gl.TRIANGLES;
    var offset = 0;
    var count = 18;
    gl.drawArrays(primitiveType, offset, count);
  }

E aqui está o resultado. Arraste a alça no círculo para rotacionar, ou, os sliders para translacionar.

Mas como isso funciona? Bem, vamos ao cálculos.

    rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
    rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Digamos que você tenha um retângulo e que você queira girá-lo. Antes de começar a rotacioná-lo, o canto superior direito está em 3.0, 9.0. Vamos escolher um ponto no círculo unitário à 30 graus no sentido horário.

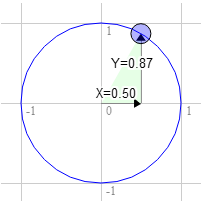
A posição no círculo é 0.50 e 0.87

   3.0 * 0.87 + 9.0 * 0.50 = 7.1
   9.0 * 0.87 - 3.0 * 0.50 = 6.3

É exatamente aonde precisamos que ele esteja

A mesma coisa se aplica para 60 graus no sentido horário

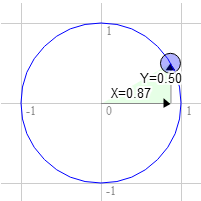
A posição no círculo é 0.87 e 0.50

   3.0 * 0.50 + 9.0 * 0.87 = 9.3
   9.0 * 0.50 - 3.0 * 0.87 = 1.9

Você pode ver que ao girar esse ponto no sentido horário, à direita, o valor X aumenta e o Y diminui. Se mantivéssemos passando 90 graus, o X começaria a ficar mais pequeno novamente e o Y começaria a ficar maior. Esse padrão nos dá a rotação.

Também existe uma outra nomenclatura para os pontos dentro de um círculo unitário. Eles são chamados de seno e cosseno. Então, para qualquer ângulo que seja fornecido, nós podemos simplesmente ver o seno e cosseno da seguinte maneira.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

Se você copiar e colar o código no seu console de JavaScript e escrever printSineAndCosignForAngle(30), você verá que s = 0.49 c = 0.87 será impresso (nota: eu arredondei os valores).

Se você colocar tudo isso junto, você será capaz de rotacionar sua geometria em qualquer ângulo que vocẽ desejar. Apenas defina a rotação com o seno e o cosseno referentes ao ângulo que você deseja.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

Aqui está uma versão que tem um ajuste de ângulo. Arraste os sliders para translacionar ou girar.

Espero que tudo isso tenha feito algum sentido pra você. A seguir, um exemplo mais simples. Escala em 2D.